RESISTÊNCIA DOS MATERIAIS
Qual a máxima tensão de cisalhamento que atua na viga ilustrada abaixo?
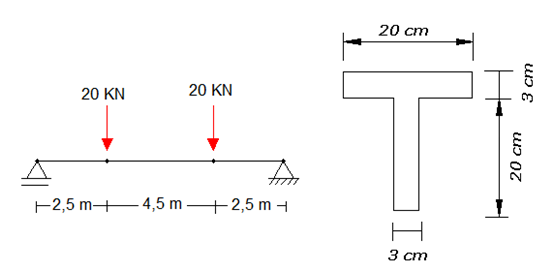
t = 5,84 MPa
t = 4,13 MPA
t = 7,03 MPa
t = 5,04 MPa
t = 6,22 MPa
Os dois elementos de aço estão interligados por uma solda de topo angulada de 60º. Determine a tensão de cisalhamento média e a tensão normal média suportada no plano da solda.
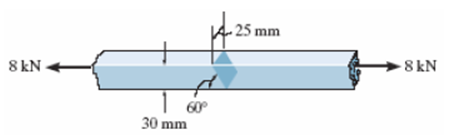
σ = 8 MPa; T=4,62 MPa
σ = 5,24 MPa; T= 10 MPa
σ = 10 MPa; T= 5,24 MPa
σ = 4 MPa; T= 2,31 MPa
σ = 4,62 MPa; T= 8 MPa
A coluna de aço A-36 (E = 200 GPa) tem área de seção transversal de 11.250 mm² e está engastada em concreto de alta resistência (E = 29 GPa), como mostra a figura. Se uma força axial de 300 kN for aplicada à coluna, determine até que distância a coluna se encurta? Seu comprimento original é 2,4 m.
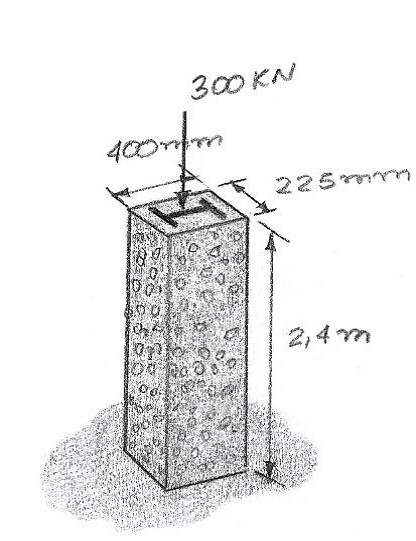
d = 0,16 mm
d = 0,18 mm
d = 0,25 mm
d = 0,20 mm
d = 0,30 mm
O eixo tem diâmetro externo de 32 mm e diâmetro interno de 25 mm. Se for submetido aos torques aplicados mostrado na figura, determine a tensão de cisalhamento máxima absoluta desenvolvida no eixo. Os mancais lisos em A e B não resistem a torque.
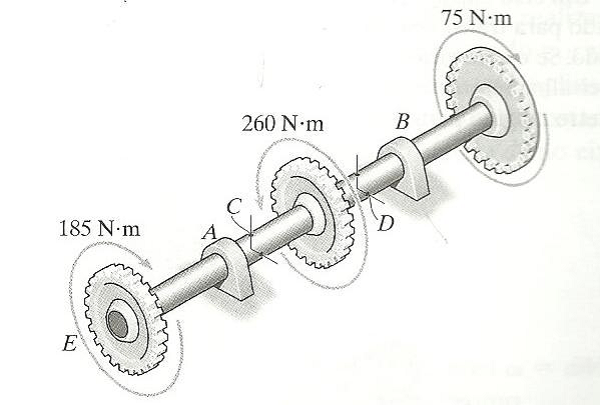
Tmáx = 50 MPa
Tmáx = 45,82 MPa
Tmáx = 44 MPa
Tmáx = 48,52 MPa
Tmáx = 46,28 MPa
O tubo é feito de plástico, tem 5 mm de espessura e as dimensões médias são mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se o tubo for submetido a um torque T = 500 N.m.
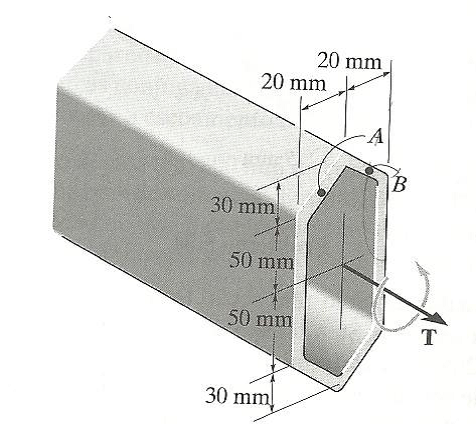
(TA) méd= 9,62 MPa e (TB) méd= 6,92 MPa
(TA) méd= 11,62 MPa e (TB) méd= 11,62 MPa
(TA) méd= 6,92 MPa e (TB) méd= 9,62 MPa
(TA) méd= 9,62 MPa e (TB) méd= 9,62 MPa
(TA) méd= 7,62 MPa e (TB) méd= 4,62 MPa
A viga de seção retangular mostrada a seguir está sujeita à distribuição de tensões admissível de 3 KN/cm². Qual o momento fletor interno na seção causado pela distribuição das tensões?
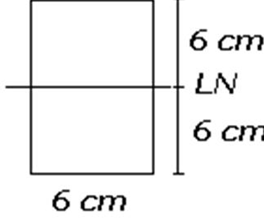
108 KN.cm
648 KN.cm
540 KN.cm
216 KN.cm
432 KN.cm
Um ensaio de tração foi executado em um corpo de prova de aço com diâmetro original 15 mm e um comprimento nominal de 30 cm. Quando uma força axial de tração de 150 kN é aplicada, a barra sofre um alongamento de 2,25 mm. Qual o módulo de elasticidade do material? Considere G = 75 GPa.
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
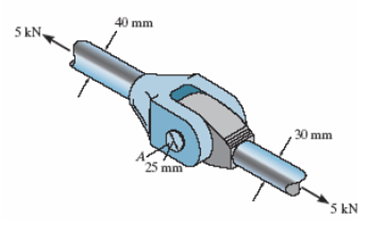
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
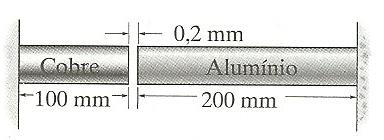
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
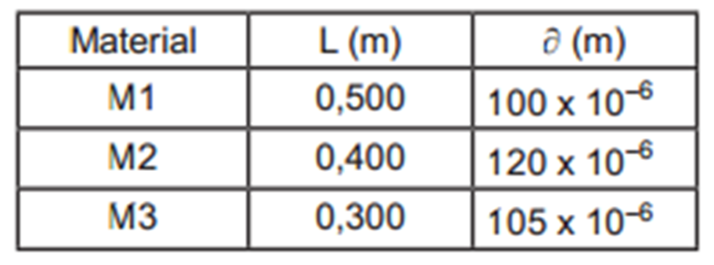Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
t = 5,84 MPa
t = 4,13 MPA
t = 7,03 MPa
t = 5,04 MPa
t = 6,22 MPa
Os dois elementos de aço estão interligados por uma solda de topo angulada de 60º. Determine a tensão de cisalhamento média e a tensão normal média suportada no plano da solda.
σ = 8 MPa; T=4,62 MPa
σ = 5,24 MPa; T= 10 MPa
σ = 10 MPa; T= 5,24 MPa
σ = 4 MPa; T= 2,31 MPa
σ = 4,62 MPa; T= 8 MPa
A coluna de aço A-36 (E = 200 GPa) tem área de seção transversal de 11.250 mm² e está engastada em concreto de alta resistência (E = 29 GPa), como mostra a figura. Se uma força axial de 300 kN for aplicada à coluna, determine até que distância a coluna se encurta? Seu comprimento original é 2,4 m.
d = 0,16 mm
d = 0,18 mm
d = 0,25 mm
d = 0,20 mm
d = 0,30 mm
O eixo tem diâmetro externo de 32 mm e diâmetro interno de 25 mm. Se for submetido aos torques aplicados mostrado na figura, determine a tensão de cisalhamento máxima absoluta desenvolvida no eixo. Os mancais lisos em A e B não resistem a torque.
Tmáx = 50 MPa
Tmáx = 45,82 MPa
Tmáx = 44 MPa
Tmáx = 48,52 MPa
Tmáx = 46,28 MPa
O tubo é feito de plástico, tem 5 mm de espessura e as dimensões médias são mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se o tubo for submetido a um torque T = 500 N.m.
(TA) méd= 9,62 MPa e (TB) méd= 6,92 MPa
(TA) méd= 11,62 MPa e (TB) méd= 11,62 MPa
(TA) méd= 6,92 MPa e (TB) méd= 9,62 MPa
(TA) méd= 9,62 MPa e (TB) méd= 9,62 MPa
(TA) méd= 7,62 MPa e (TB) méd= 4,62 MPa
A viga de seção retangular mostrada a seguir está sujeita à distribuição de tensões admissível de 3 KN/cm². Qual o momento fletor interno na seção causado pela distribuição das tensões?
108 KN.cm
648 KN.cm
540 KN.cm
216 KN.cm
432 KN.cm
Um ensaio de tração foi executado em um corpo de prova de aço com diâmetro original 15 mm e um comprimento nominal de 30 cm. Quando uma força axial de tração de 150 kN é aplicada, a barra sofre um alongamento de 2,25 mm. Qual o módulo de elasticidade do material? Considere G = 75 GPa.
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
σ = 8 MPa; T=4,62 MPa
σ = 5,24 MPa; T= 10 MPa
σ = 10 MPa; T= 5,24 MPa
σ = 4 MPa; T= 2,31 MPa
σ = 4,62 MPa; T= 8 MPa
A coluna de aço A-36 (E = 200 GPa) tem área de seção transversal de 11.250 mm² e está engastada em concreto de alta resistência (E = 29 GPa), como mostra a figura. Se uma força axial de 300 kN for aplicada à coluna, determine até que distância a coluna se encurta? Seu comprimento original é 2,4 m.
d = 0,16 mm
d = 0,18 mm
d = 0,25 mm
d = 0,20 mm
d = 0,30 mm
O eixo tem diâmetro externo de 32 mm e diâmetro interno de 25 mm. Se for submetido aos torques aplicados mostrado na figura, determine a tensão de cisalhamento máxima absoluta desenvolvida no eixo. Os mancais lisos em A e B não resistem a torque.
Tmáx = 50 MPa
Tmáx = 45,82 MPa
Tmáx = 44 MPa
Tmáx = 48,52 MPa
Tmáx = 46,28 MPa
O tubo é feito de plástico, tem 5 mm de espessura e as dimensões médias são mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se o tubo for submetido a um torque T = 500 N.m.
(TA) méd= 9,62 MPa e (TB) méd= 6,92 MPa
(TA) méd= 11,62 MPa e (TB) méd= 11,62 MPa
(TA) méd= 6,92 MPa e (TB) méd= 9,62 MPa
(TA) méd= 9,62 MPa e (TB) méd= 9,62 MPa
(TA) méd= 7,62 MPa e (TB) méd= 4,62 MPa
A viga de seção retangular mostrada a seguir está sujeita à distribuição de tensões admissível de 3 KN/cm². Qual o momento fletor interno na seção causado pela distribuição das tensões?
108 KN.cm
648 KN.cm
540 KN.cm
216 KN.cm
432 KN.cm
Um ensaio de tração foi executado em um corpo de prova de aço com diâmetro original 15 mm e um comprimento nominal de 30 cm. Quando uma força axial de tração de 150 kN é aplicada, a barra sofre um alongamento de 2,25 mm. Qual o módulo de elasticidade do material? Considere G = 75 GPa.
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
d = 0,16 mm
d = 0,18 mm
d = 0,25 mm
d = 0,20 mm
d = 0,30 mm
O eixo tem diâmetro externo de 32 mm e diâmetro interno de 25 mm. Se for submetido aos torques aplicados mostrado na figura, determine a tensão de cisalhamento máxima absoluta desenvolvida no eixo. Os mancais lisos em A e B não resistem a torque.
Tmáx = 50 MPa
Tmáx = 45,82 MPa
Tmáx = 44 MPa
Tmáx = 48,52 MPa
Tmáx = 46,28 MPa
O tubo é feito de plástico, tem 5 mm de espessura e as dimensões médias são mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se o tubo for submetido a um torque T = 500 N.m.
(TA) méd= 9,62 MPa e (TB) méd= 6,92 MPa
(TA) méd= 11,62 MPa e (TB) méd= 11,62 MPa
(TA) méd= 6,92 MPa e (TB) méd= 9,62 MPa
(TA) méd= 9,62 MPa e (TB) méd= 9,62 MPa
(TA) méd= 7,62 MPa e (TB) méd= 4,62 MPa
A viga de seção retangular mostrada a seguir está sujeita à distribuição de tensões admissível de 3 KN/cm². Qual o momento fletor interno na seção causado pela distribuição das tensões?
108 KN.cm
648 KN.cm
540 KN.cm
216 KN.cm
432 KN.cm
Um ensaio de tração foi executado em um corpo de prova de aço com diâmetro original 15 mm e um comprimento nominal de 30 cm. Quando uma força axial de tração de 150 kN é aplicada, a barra sofre um alongamento de 2,25 mm. Qual o módulo de elasticidade do material? Considere G = 75 GPa.
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
Tmáx = 50 MPa
Tmáx = 45,82 MPa
Tmáx = 44 MPa
Tmáx = 48,52 MPa
Tmáx = 46,28 MPa
O tubo é feito de plástico, tem 5 mm de espessura e as dimensões médias são mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se o tubo for submetido a um torque T = 500 N.m.
(TA) méd= 9,62 MPa e (TB) méd= 6,92 MPa
(TA) méd= 11,62 MPa e (TB) méd= 11,62 MPa
(TA) méd= 6,92 MPa e (TB) méd= 9,62 MPa
(TA) méd= 9,62 MPa e (TB) méd= 9,62 MPa
(TA) méd= 7,62 MPa e (TB) méd= 4,62 MPa
A viga de seção retangular mostrada a seguir está sujeita à distribuição de tensões admissível de 3 KN/cm². Qual o momento fletor interno na seção causado pela distribuição das tensões?
108 KN.cm
648 KN.cm
540 KN.cm
216 KN.cm
432 KN.cm
Um ensaio de tração foi executado em um corpo de prova de aço com diâmetro original 15 mm e um comprimento nominal de 30 cm. Quando uma força axial de tração de 150 kN é aplicada, a barra sofre um alongamento de 2,25 mm. Qual o módulo de elasticidade do material? Considere G = 75 GPa.
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
(TA) méd= 9,62 MPa e (TB) méd= 6,92 MPa
(TA) méd= 11,62 MPa e (TB) méd= 11,62 MPa
(TA) méd= 6,92 MPa e (TB) méd= 9,62 MPa
(TA) méd= 9,62 MPa e (TB) méd= 9,62 MPa
(TA) méd= 7,62 MPa e (TB) méd= 4,62 MPa
A viga de seção retangular mostrada a seguir está sujeita à distribuição de tensões admissível de 3 KN/cm². Qual o momento fletor interno na seção causado pela distribuição das tensões?
108 KN.cm
648 KN.cm
540 KN.cm
216 KN.cm
432 KN.cm
Um ensaio de tração foi executado em um corpo de prova de aço com diâmetro original 15 mm e um comprimento nominal de 30 cm. Quando uma força axial de tração de 150 kN é aplicada, a barra sofre um alongamento de 2,25 mm. Qual o módulo de elasticidade do material? Considere G = 75 GPa.
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
108 KN.cm
648 KN.cm
540 KN.cm
216 KN.cm
432 KN.cm
Um ensaio de tração foi executado em um corpo de prova de aço com diâmetro original 15 mm e um comprimento nominal de 30 cm. Quando uma força axial de tração de 150 kN é aplicada, a barra sofre um alongamento de 2,25 mm. Qual o módulo de elasticidade do material? Considere G = 75 GPa.
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
113,18 GPa
110,16 GPa
111,74 GPa
107,35 GPa
125,16 GPa
O acoplamento de gancho e haste está sujeito a uma força de tração de 5 kN. Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
σ40 = 3.979 MPa; σ30 = 5.074 MPa; T = 7.093 MPa
σ40 = 7.074 MPa; σ30 = 3.979 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 7.074 MPa; T = 5.093 MPa
σ40 = 3.979 MPa; σ30 = 5.093 MPa; T = 7.074 MPa
σ40 = 5.093 MPa; σ30 = 3.979 MPa; T = 7.074 MPa
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa. Determine a tensão normal média em cada haste se T2 = 95 °C.
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa
Em ensaios de tração realizados com três materiais, foram encontrados os seguintes valores de deformação (∂) correspondentes aos respectivos comprimentos iniciais (L):
Ao se analisar a deformação específica normal (ε) de cada material, tem-se que:
T = 78,65 MPa
T = 100 MPa
T = 45,77 MPa
T = 87,65 MPa
T = 65,87 MPa